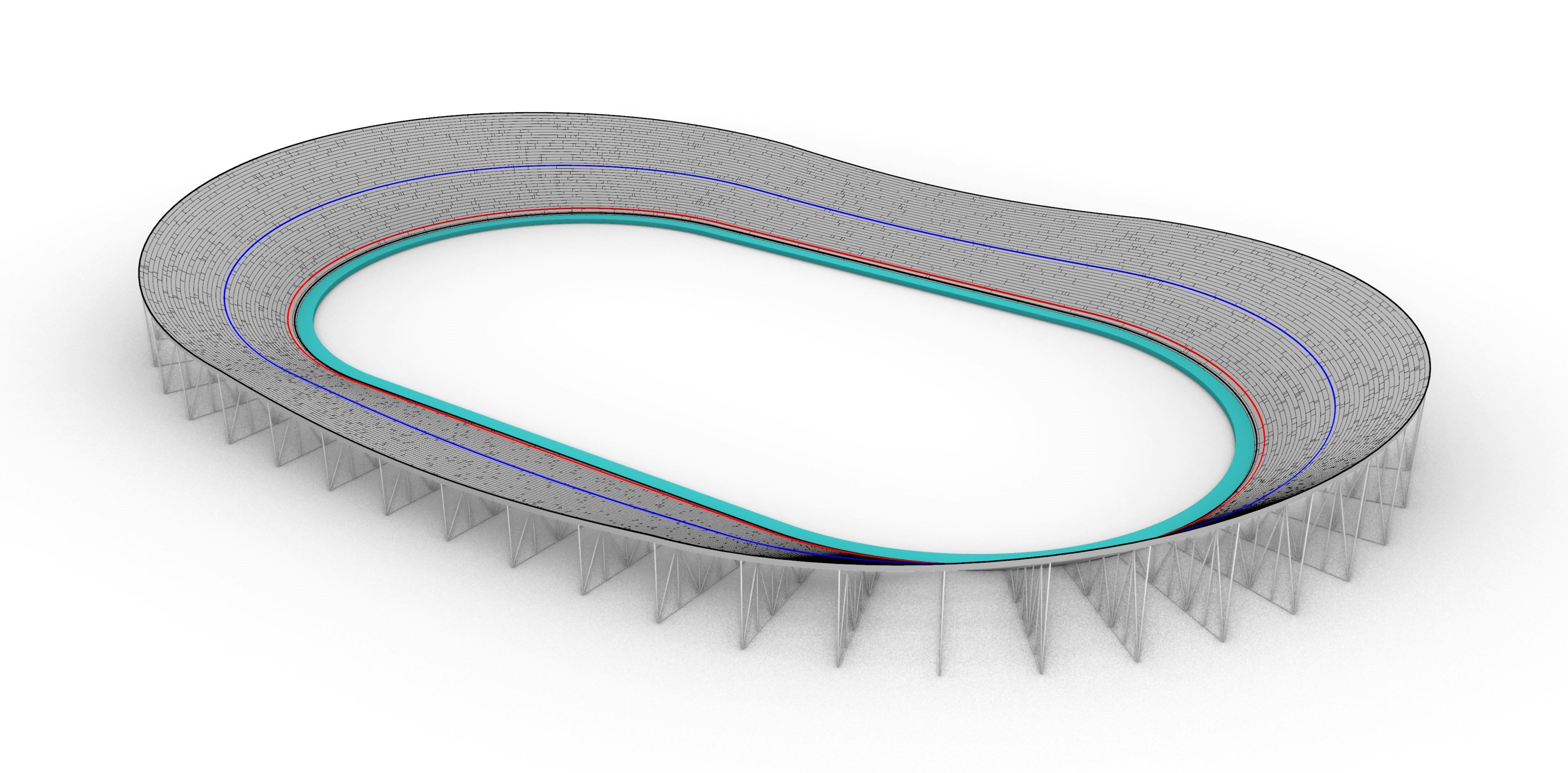
While many programs have some measure of spatial flexibility in their execution, there exist certain programs which are defined by ultra-specific spatial requirements, and often these requirements are (literally) central to the basic usability of the building. There is no room for creative license with regard to the dimensions of a basketball or tennis court, for example, and the design of the buildings that house them must hold those dimensions absolutely sacrosanct. Other similar programs, like baseball and soccer fields, are nearly as constrained but have a measure of flexibility built in to their function.

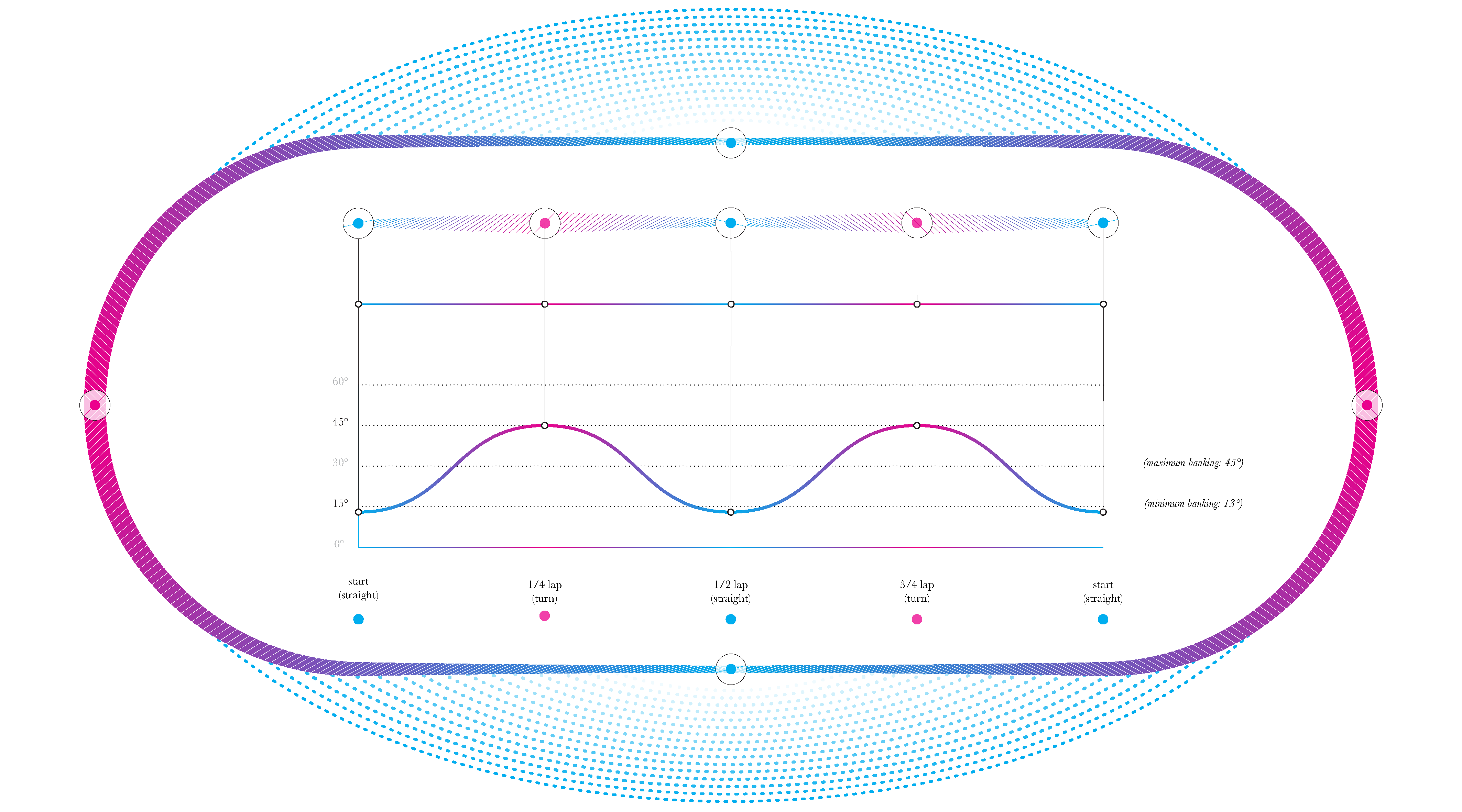
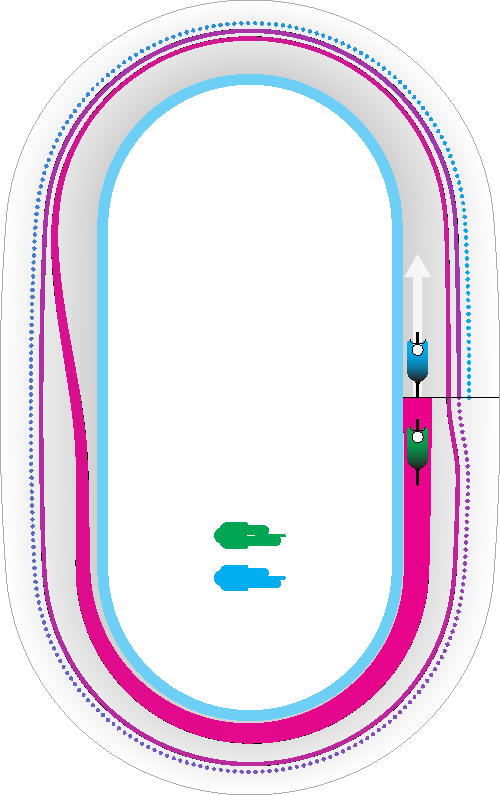
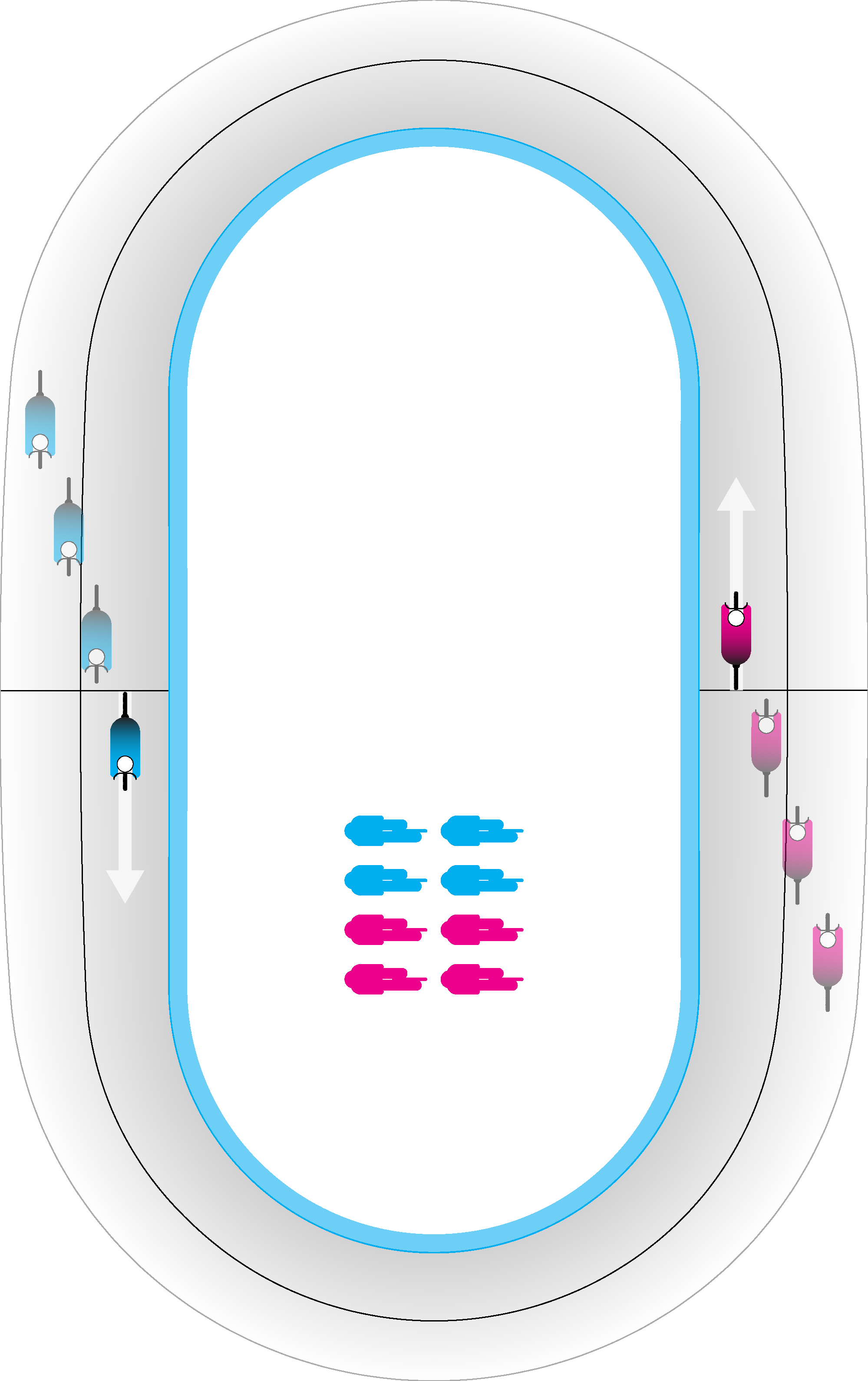
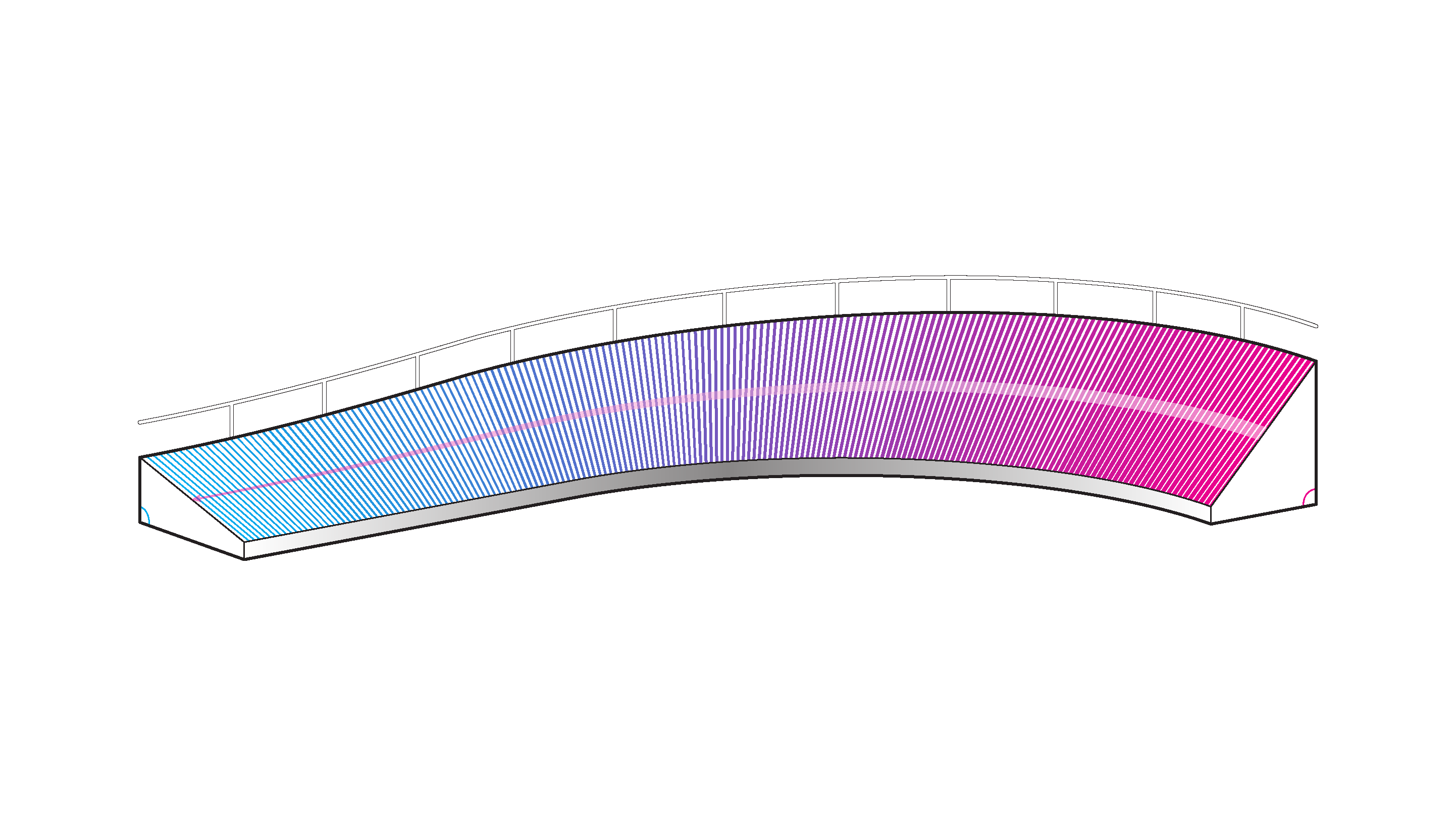
An Olympic velodrome must be 250m in circumference at the measurement line (just inside the innermost edge of the track band), but its length and width are highly variable (within upper and lower bounds), as are the banking angles of the straights and corners. The physics of riding the track dictate that a higher banking angle requires a higher speed (and stronger riders) in order to remain upright, but also allows for much quicker accelerations in sprints and other events in which descending the banking can be used to generate speed.